Kitobni o'qish: «Нейросети. Обработка аудиоданных»

Глава 1: Введение в обработку аудиоданных с использованием нейросетей

1.1. Обзор основных концепций нейросетей и их применение в обработке аудиоданных

Нейронные сети (или нейросети) – это класс алгоритмов машинного обучения, вдохновленных работой человеческого мозга. Они используются для обработки данных и решения различных задач, включая обработку аудиоданных. Кратко рассмотрим основные концепции нейросетей и их применение в обработке аудиоданных:

1. Искусственный нейрон: Искусственные нейроны, которые составляют основу нейросетей, можно сравнить с строительными блоками, схожими с нейронами в человеческом мозге. Каждый искусственный нейрон принимает входные сигналы, выполняет математические операции над ними, такие как взвешивание и суммирование, и затем передает результат следующему слою нейронов. Это происходит во всех слоях нейросети, создавая сложную сеть, которая способна обучаться и выполнять разнообразные задачи, от распознавания образов до обработки аудио и текстовых данных. Искусственные нейроны и их взаимодействие позволяют нейросетям аппроксимировать сложные функции и извлекать паттерны и зависимости в данных, что делает их мощным инструментом в мире машинного обучения и искусственного интеллекта.

2. Многослойная нейронная сеть: Многослойные нейронные сети представляют собой многократное повторение базовых строительных блоков – искусственных нейронов, и они являются ключевой архитектурой в мире глубокого обучения. Эти сети состоят из нескольких слоев, где входные данные поступают во входной слой, затем проходят через один или несколько скрытых слоев, и наконец, результаты передаются на выходной слой. Многослойные нейронные сети позволяют изучать сложные и абстрактные зависимости в данных. Это особенно важно для задач, где простые модели не могут справиться с сложными взаимосвязями, такими как распознавание образов, обработка текстов, анализ аудиоданных и другие задачи в машинном обучении. Глубокие нейронные сети, включая сверточные и рекуррентные архитектуры, применяются в разнообразных областях и продолжают демонстрировать впечатляющие результаты в сложных задачах анализа данных.

3. Обучение с учителем: Обучение с учителем – ключевой этап в обучении нейросетей, где модель учится на основе размеченных данных. Это означает, что для каждого входа в сеть имеется соответствующий выход, который известен заранее. Алгоритмы обучения, такие как обратное распространение ошибки, используются для коррекции весов и параметров сети таким образом, чтобы минимизировать разницу между предсказанными значениями и фактическими данными. Это происходит через многократные итерации, где сеть улучшает свою способность делать предсказания на новых данных. Обучение с учителем является фундаментальным методом в машинном обучении и позволяет нейросетям адаптироваться к разнообразным задачам, включая классификацию, регрессию, распознавание образов, и многое другое.

4. Функции активации: Функции активации играют ключевую роль в работе нейронных сетей, определяя, как нейроны реагируют на входные данные. Популярные функции активации включают в себя ReLU (Rectified Linear Unit), сигмоиду и гиперболический тангенс. Эти функции добавляют нелинейность в модель, что имеет фундаментальное значение, так как многие реальные задачи характеризуются сложными и нелинейными зависимостями. Нелинейность функций активации позволяет нейросетям обучаться и извлекать сложные паттерны в данных. Например, функция ReLU поддерживает активацию нейронов только при положительных значениях, что позволяет сети выделять важные признаки в данных и игнорировать шум. Этот аспект делает функции активации важными компонентами в процессе обучения нейросетей и в разработке более точных и эффективных моделей.

5. Сверточные нейронные сети (CNN): Сверточные нейронные сети (CNN) – это специализированный класс нейросетей, который показал выдающуюся эффективность в обработке изображений и аудиоданных. Они применяют сверточные слои для автоматического выделения важных признаков из входных данных, что особенно важно в аудиоанализе, где высокочастотные и временные характеристики могут содержать ценную информацию. Пулинг слои используются для уменьшения размерности данных и извлечения ключевых аспектов. CNN широко применяются в задачах, таких как распознавание речи и анализ аудиосигналов, их способность автоматически извлекать признаки из аудиоданных сделала их важным инструментом в мире машинного обучения и обработки сигналов.

6. Рекуррентные нейронные сети (RNN): Рекуррентные нейронные сети (RNN) представляют собой класс нейросетей, спроектированный специально для работы с последовательными данными. Они обладают внутренней памятью, что позволяет им учитывать зависимости в последовательностях данных. Это свойство делает их идеальными для задач, таких как анализ текста и распознавание речи, где важно учесть контекст и последовательность слов или фраз. RNN способны моделировать долгосрочные зависимости в данных и могут быть использованы в широком спектре приложений, где последовательности играют важную роль, включая машинный перевод, генерацию текста, анализ временных рядов и многое другое.

7. Долгая краткосрочная память (LSTM) и Градиентные рекуррентные единицы (GRU): Долгая краткосрочная память (LSTM) и градиентные рекуррентные единицы (GRU) представляют собой эволюцию рекуррентных нейронных сетей (RNN) и добавляют важную функциональность в обработку последовательных данных. Эти архитектуры позволяют нейросетям учить долгосрочные зависимости в данных, такие как контекст и зависимости, которые растягиваются на длительные последовательности. LSTM и GRU особенно полезны в задачах, где важно учитывать информацию из давно предшествующих элементов последовательности, таких как машинный перевод, генерация текста и анализ временных рядов. Эти архитектуры предоставляют нейросетям способность обрабатывать сложные и долгосрочные зависимости, делая их важными инструментами в обработке последовательных данных.

Применение нейросетей в обработке аудиоданных:

1. Распознавание речи: Распознавание речи с помощью нейросетей – это, как волшебство, которое позволяет компьютерам понимать, что мы говорим. Это работает так: сперва компьютер анализирует звуки из аудиофайла, и здесь нам помогают сверточные нейронные сети, они вылавливают особенности в звуках, похожие на то, как мы распознаем лица на фотографиях. Затем, рекуррентные нейронные сети делают важную вещь: они учитывают, как слова связаны между собой в предложениях, что очень важно, потому что речь – это последовательность звуков. После этого компьютер обучается на большом количестве аудиозаписей, где к каждой записи прикреплен текст. Он старается минимизировать ошибки и понимать речь как можно лучше. В конечном итоге, это позволяет создавать голосовых ассистентов, системы распознавания речи в автомобилях и многое другое, что делает нашу жизнь проще и удобнее.

2. Обработка аудиосигналов: Нейросети играют важную роль в обработке аудиосигналов, преображая звуки в цифровой мир. Они могут быть использованы для фильтрации нежелательных шумов в аудиозаписях, что полезно, например, при записи в шумных окружениях или в студийных условиях. Нейросети также способны значительно улучшить качество аудиозаписей, устраняя искажения или шумы. Кроме того, они могут генерировать аудио, что находит применение в сферах, таких как музыкальное творчество и синтез речи. Эти возможности нейросетей делают их мощными инструментами в обработке и улучшении аудиоданных, а также в создании новых звуковых контентов.

3. Анализ музыки: Нейросети открывают перед нами захватывающие перспективы в анализе музыки. Они способны классифицировать жанры музыки, что помогает музыкальным платформам и службам рекомендаций подбирать подходящие треки для пользователей. Кроме того, нейросети могут определять настроение музыки, что полезно для создания плейлистов и музыкальных рекомендаций. Один из самых захватывающих аспектов – способность нейросетей создавать музыку. Генеративные модели, такие как GANs и вариационные автоэнкодеры, могут создавать оригинальные композиции, что ставит перед нами новые горизонты в творчестве и музыкальной индустрии. Нейросети позволяют сделать музыку ещё более доступной и вдохновляют музыкантов и аудиторию на новые творческие эксперименты.

4. Обнаружение аномалий: Поле применения нейросетей для обнаружения аномалий в аудиоданных охватывает множество областей. В медицине, они могут помочь в раннем обнаружении звуков, связанных с болезнями, такими как стетоскопические звуки легких, сердечные шумы или акустические признаки аритмии. В промышленности, нейросети используются для обнаружения аномалий в машинных звуках, что помогает в предотвращении отказов оборудования и повышении эффективности технического обслуживания. В системах безопасности, таких как видеонаблюдение и системы домашней безопасности, нейросети способны реагировать на необычные звуковые сигналы, что повышает уровень защиты и предотвращает инциденты.

Кроме того, нейросети могут быть обучены для анализа акустических данных в реальном времени. Это имеет большое значение в сферах, где быстрая реакция на аномалии критически важна, таких как пожарная безопасность, слежение за звуками, связанными с авариями на дорогах, и обнаружение звуковых событий, связанных с криминальной деятельностью.

5. Синтез речи: Нейросети играют важную роль в области синтеза речи, позволяя компьютерам создавать аудиосигналы, которые звучат как человеческая речь. Они могут преобразовывать текстовую информацию в звуковые данные, что полезно для создания разнообразных приложений, включая голосовых ассистентов, аудиокниги, системы озвучивания текста, системы автоматического чтения для лиц с ограниченными возможностями, и даже в аудиовизуальных эффектах для фильмов и игр. Технологии синтеза речи на основе нейросетей становятся всё более реалистичными и естественными, приближаясь к качеству человеческой речи и расширяя возможности автоматизированного генерирования и обработки аудиоконтента.

Нейросети продемонстрировали значительные успехи в обработке аудиоданных, и их использование продолжает расширяться в различных областях, включая медицину, автомобильную промышленность, развлечения и коммуникации.

1.2. Основы аудиосигналов и их представления в цифровой форме

Для понимания обработки аудиоданных с использованием нейросетей важно ознакомиться с основами аудиосигналов и их представления в цифровой форме.

Аудиосигнал представляет собой колебания во времени, которые возникают при передаче звука через воздух или другую среду. Аудиосигнал может быть слышимым (например, человеческая речь или музыка) или неслышимым (например, ультразвуковой сигнал). Он характеризуется частотой, амплитудой и временем. Частота определяет, как быстро колебания происходят в секунду и измеряется в герцах (Гц). Амплитуда определяет высоту колебаний и влияет на громкость сигнала. Время отражает последовательность колебаний.

Представление аудиосигнала в цифровой форме осуществляется путем дискретизации. Это процесс измерения значения аудиосигнала в разные моменты времени и его записи в цифровой форме. Он включает в себя два ключевых параметра:

1. Частота дискретизации (sample rate):Частота дискретизации (sample rate) в аудиоданных определяет, сколько раз аудиосигнал измеряется в секунду. Измеряется в герцах (Гц). Более высокая частота дискретизации обеспечивает более точное представление аудиосигнала, но при этом требуется больше памяти для хранения и обработки данных. Это важный параметр при работе с аудиоданными, так как он влияет на качество и точность представления сигнала в цифровой форме.

2. Разрешение бита (bit depth): Разрешение бита (bit depth) в аудиоданных указывает на количество битов, используемых для представления значения каждого отсчета аудиосигнала. Этот параметр важен, так как он влияет на динамику сигнала и его качество. Высокое разрешение бита позволяет сохранить больше информации о изменениях амплитуды звука в течение времени, что обеспечивает более точное и высококачественное звучание. Например, CD-аудио использует разрешение бита 16 бит, что позволяет записать широкий диапазон амплитуд и получить высококачественный звук. Однако более высокое разрешение бита, такое как 24 бита или более, может быть использовано для аудиофайлов высшего разрешения, чтобы сохранить даже более детальную информацию о динамике и обеспечить аудиофайлы выдающегося качества.

Цифровое представление аудиосигнала является фундаментальным для его обработки и анализа с использованием компьютеров и других устройств. Преобразование аналогового аудиосигнала в цифровую форму позволяет его хранить, передавать и обрабатывать с легкостью. Для обработки аудиосигналов с помощью нейросетей, аудиоданные часто преобразуются в спектрограммы. Спектрограммы представляют спектральное содержание сигнала в зависимости от времени, позволяя анализировать различные частоты, как они меняются во времени. Это дает возможность автоматически выделять важные аудиофункции, такие как мелодии, аккорды, речь или звуковые события, и использовать их для различных задач, включая анализ и классификацию звуков, распознавание речи и даже создание нового аудиоконтента. Спектрограммы являются мощным инструментом для работы с аудиоданными и позволяют нейросетям обнаруживать и извлекать сложные паттерны и зависимости в аудиосигналах.

Концепции и термины, упомянутые в главе

Аудиосигнал – кодебания воздуха или другой среды, используемые для передачи звука.

Частота дискретизации (sample rate) – количество измерений аудиосигнала в секунду, измеряется в герцах (Гц).

Разрешение бита (bit depth) – количество битов, используемых для представления значения каждого отсчета аудиосигнала.

Спектрограмма – графическое представление спектрального содержания аудиосигнала в зависимости от времени.

Спектральное содержание – распределение амплитуд различных частотных компонентов в аудиосигнале.

Аналоговый сигнал – неприрывный сигнал, представляющий собой непрерывное изменение параметров, таких как амплитуда и частота.

Цифровой сигнал – сигнал, представленный в цифровой (дискретной) форме, путем дискретизации аналогового сигнала.

Динамика сигнала – разница между минимальной и максимальной амплитудой в аудиосигнале.

Амплитуда – мера высоты колебаний аудиосигнала, влияющая на громкость звука.

Эти термины являются основополагающими для понимания обработки аудиоданных и их преобразования в цифровую форму для последующей обработки нейросетями.

Глава 2: Основы аудиообработки

2.1. Обзор основных понятий аудиообработки, включая амплитуду, частоту, фазу и спектр

Аудиообработка включает в себя ряд важных понятий и концепций, которые помогают понять, как работает обработка и анализ аудиоданных. Рассмотрим основные из них:

1. Амплитуда: Амплитуда аудиосигнала является одним из его наиболее фундаментальных свойств. Это мера силы колебаний воздушных молекул или другой среды, которая создает звук. Чем больше амплитуда, тем сильнее колебания, и, следовательно, тем громче звучит звук. Измеряется в децибелах (дБ), что представляет собой логарифмическую шкалу, отражающую отношение амплитуды звука к определенному эталонному уровню, как правило, порогу слышимости человеческого уха.

Амплитуда играет ключевую роль в аудиоинженерии и обработке аудиосигналов. Она позволяет устанавливать громкость аудиозаписей, управлять уровнями громкости в звуковой продукции и создавать эффекты звуковой динамики, такие как атака и релиз в музыке. Амплитуда также важна в задачах обработки и улучшения аудиосигналов, где уровни амплитуды могут быть регулированы, чтобы устранить шум или усилить желаемые акустические события. Таким образом, амплитуда является неотъемлемой частью аудиоинженерии и аудиообработки, оказывая влияние на качество и восприятие звука.

2. Частота: Частота в аудиообработке представляет собой ключевой параметр, определяющий, как быстро звуковая волна колеблется в течение одной секунды. Это измерение выражается в герцах (Гц) и описывает, насколько быстро аудиоволна переходит от одной точки максимальной амплитуды к другой. Чем выше частота, тем более высокие и частотные звуки воспринимаются.

– Низкие частоты обычно соответствуют басовым звукам. Это глубокие, гулкие звуки, которые создаются медленными колебаниями. Низкие частоты играют важную роль в формировании музыкальных басов и основных ритмов.

– Средние частоты охватывают диапазон звуков от нижних голосовых нот до более высоких инструментов, таких как гитара и скрипка. Они вносят вклад в мелодию и гармонию.

– Высокие частоты представляют собой тонкие нюансы и детали в аудиосигнале. Они определяют звуки, такие как сверчки, мелкие перкуссионные инструменты и высокие ноты в вокале.

Частота важна для аудиоинженерии и музыкального производства, так как позволяет контролировать тон и характер звучания. Понимание частотных характеристик аудиосигнала помогает в настройке эквалайзеров, фильтрации нежелательных частот и создании желаемого звучания. Также частотный анализ может использоваться для задач, таких как распознавание речи и классификация аудиоданных.

3. Фаза: Фаза в аудиообработке представляет собой важное понятие, связанное с текущим угловым положением звуковой волны в определенный момент времени. Это измерение выражается в радианах и определяет, на какой стадии колебаний находится звуковая волна в данный момент. Понимание фазы помогает определить, в какой момент времени происходит начало или конец колебаний звуковой волны.

Фаза может оказывать влияние на звучание и взаимодействие звуковых волн, особенно при их смешивании или интерференции. Когда две звуковые волны с разной фазой встречаются, они могут усилить друг друга (конструктивная интерференция) или уменьшить амплитуду (деструктивная интерференция), что важно для формирования звучания и звуковых эффектов.

Фаза также играет важную роль в синтезе звука и создании аудиоэффектов. Манипуляции фазой могут использоваться для изменения звучания, включая создание фазовых эффектов, таких как фазовая модуляция и фазовая инверсия. Понимание фазы важно для звукозаписи, музыкального производства и аудиоинженерии, так как она позволяет более точно контролировать и формировать звучание аудиосигналов, а также создавать разнообразные аудиоэффекты.

4. Спектр: Спектр аудиосигнала представляет собой важный инструмент в аудиообработке и аудиоанализе. Он разбивает аудиосигнал на его составляющие частоты, что означает, что каждая частота в спектре представляет собой определенную частотную компоненту, присутствующую в сигнале. Спектр также предоставляет информацию о том, с какой амплитудой каждая частота представлена в аудиосигнале, что позволяет определить вклад каждой частоты в звучание сигнала.

Анализ спектра имеет широкое практическое применение в аудиообработке. Он позволяет выполнять задачи, такие как эквалайзинг (регулирование частотных компонент), обнаружение и устранение шумовых составляющих, анализ и классификацию аудиосигналов. Для визуализации спектра аудиосигнала часто используется специальная диаграмма, называемая спектрограммой, которая показывает, как меняется спектр в зависимости от времени. Анализ спектра играет важную роль в аудиоинженерии, музыкальном производстве и обработке звука, помогая инженерам и артистам более точно понимать и манипулировать звучанием аудиосигналов.

Эти понятия являются фундаментальными для аудиообработки и аудиоанализа. Они позволяют понять и манипулировать характеристиками звуковых сигналов, что может быть важным при решении различных задач, включая фильтрацию, усиление, сжатие, анализ и синтез звука.

2.2. Рассмотрение методов анализа аудиосигналов, таких как преобразование Фурье и вейвлет-преобразование

Для анализа аудиосигналов и выделения их характеристик используются различные методы, включая преобразование Фурье и вейвлет-преобразование.

Преобразование Фурье

Преобразование Фурье (или Фурье-преобразование) представляет собой ключевой метод анализа аудиосигналов и является неотъемлемой частью современной аудиообработки и аудиоанализа. Давайте более подробно рассмотрим этот метод и его применение.

Принцип Преобразования Фурье:

Принцип Преобразования Фурье основан на математическом представлении аудиосигнала в частотной области. Давайте рассмотрим его математическую суть более подробно.

Предположим, у нас есть аудиосигнал, представленный как функция амплитуды от времени, обозначим его как f(t), где t – время. Преобразование Фурье этого сигнала позволяет разложить его на сумму гармонических сигналов разных частот. Математически это представляется следующим образом:

Интуитивно, этот интеграл анализирует, как разные частоты ω влияют на исходный сигнал. Результатом является функция спектра, которая показывает, какие частоты присутствуют в сигнале и с какой амплитудой. Таким образом, Преобразование Фурье предоставляет спектральное представление сигнала, что позволяет анализировать его частотные компоненты.

Преобразование Фурье является мощным инструментом для анализа аудиосигналов, позволяя разложить сложные сигналы на их спектральные составляющие и делая возможным их детальное изучение и обработку.

Преобразование времени в частоту:

Преобразование Фурье представляет позволяет перейти от временного представления сигнала к его спектральному представлению. Это преобразование исследует, какие частоты содержатся в аудиосигнале и с какой амплитудой они присутствуют. Для понимания этого принципа, рассмотрим его более подробно, сравнивая временное и частотное представление аудиосигнала.

Временное представление:

Временное представление аудиосигнала показывает, как меняется амплитуда сигнала в зависимости от времени. Если вы представите звуковой сигнал во временной области, то у вас будет график, где по горизонтальной оси будет время, а по вертикальной – амплитуда звука. Это представление подходит для изучения того, как звук меняется с течением времени.

Частотное представление:

Преобразование Фурье переводит этот временной сигнал в частотное представление. Оно разбивает сигнал на различные частоты, которые его составляют, и показывает, какие частоты присутствуют и с какой амплитудой. В частотном представлении вы уже не видите, как амплитуда меняется во времени, но зато можете точно определить, какие частоты преобладают в сигнале.

Пример музыкальной ноты:

Для наглядного примера представьте себе музыкальную ноту, например, ля (A) на гитаре. Во временной области вы увидите график, который колеблется вверх и вниз с определенной частотой. Эта частота представляет основную частоту ноты ля. Однако, помимо основной частоты, в этом звуке также присутствуют высшие гармоники, которые кратны основной частоте. Преобразование Фурье разложит этот сигнал на его основную частоту и гармоники, позволяя точно определить, какие компоненты составляют этот звук.

Преобразование Фурье позволяет перейти от временного анализа аудиосигнала к его частотному анализу, что является неотъемлемой частью аудиообработки и спектрального анализа аудиоданных.

Практическое применение:

Преобразование Фурье находит широкое применение в аудиообработке. Например, при помощи него можно:

– Определить основную частоту в аудиосигнале, что полезно при тюнинге музыкальных инструментов.

– Выделять гармоники и устанавливать их амплитуды для синтеза звука.

– Анализировать частотный спектр аудиосигнала для обнаружения шумовых компонент и фильтрации нежелательных частот.

– Выполнять спектральную классификацию и распознавание аудиосигналов.

Давайте рассмотрим пример задачи, в которой мы используем Преобразование Фурье для анализа аудиосигнала и визуализируем его спектральное представление с помощью Python. В этом примере мы будем использовать библиотеку NumPy для вычислений и библиотеку Matplotlib для визуализации.

```python

import numpy as np

import matplotlib.pyplot as plt

# Создаем симулированный аудиосигнал (например, синусоиду)

sample_rate = 1000 # Частота дискретизации в Гц

duration = 1.0 # Продолжительность сигнала в секундах

t = np.linspace(0, duration, int(sample_rate * duration), endpoint=False)

frequency = 5 # Частота синусоиды в Гц

signal = np.sin(2 * np.pi * frequency * t)

# Выполняем Преобразование Фурье

fft_result = np.fft.fft(signal)

freqs = np.fft.fftfreq(len(fft_result), 1 / sample_rate) # Частоты

# Визуализируем спектральное представление

plt.figure(figsize=(10, 4))

plt.subplot(121)

plt.plot(t, signal)

plt.title('Временное представление аудиосигнала')

plt.xlabel('Время (с)')

plt.ylabel('Амплитуда')

plt.subplot(122)

plt.plot(freqs, np.abs(fft_result))

plt.title('Спектральное представление аудиосигнала')

plt.xlabel('Частота (Гц)')

plt.ylabel('Амплитуда')

plt.xlim(0, 20) # Ограничиваем частотный диапазон

plt.show()

```

В этом примере мы создаем синусоидальный аудиосигнал, выполняем Преобразование Фурье для анализа его спектральных компонент, и визуализируем результаты. Первый график показывает временное представление сигнала, а второй график показывает спектральное представление, выделяя основную частоту синусоиды.

Вы можете экспериментировать с различными сигналами и частотами, чтобы лучше понять, как Преобразование Фурье позволяет анализировать аудиосигналы в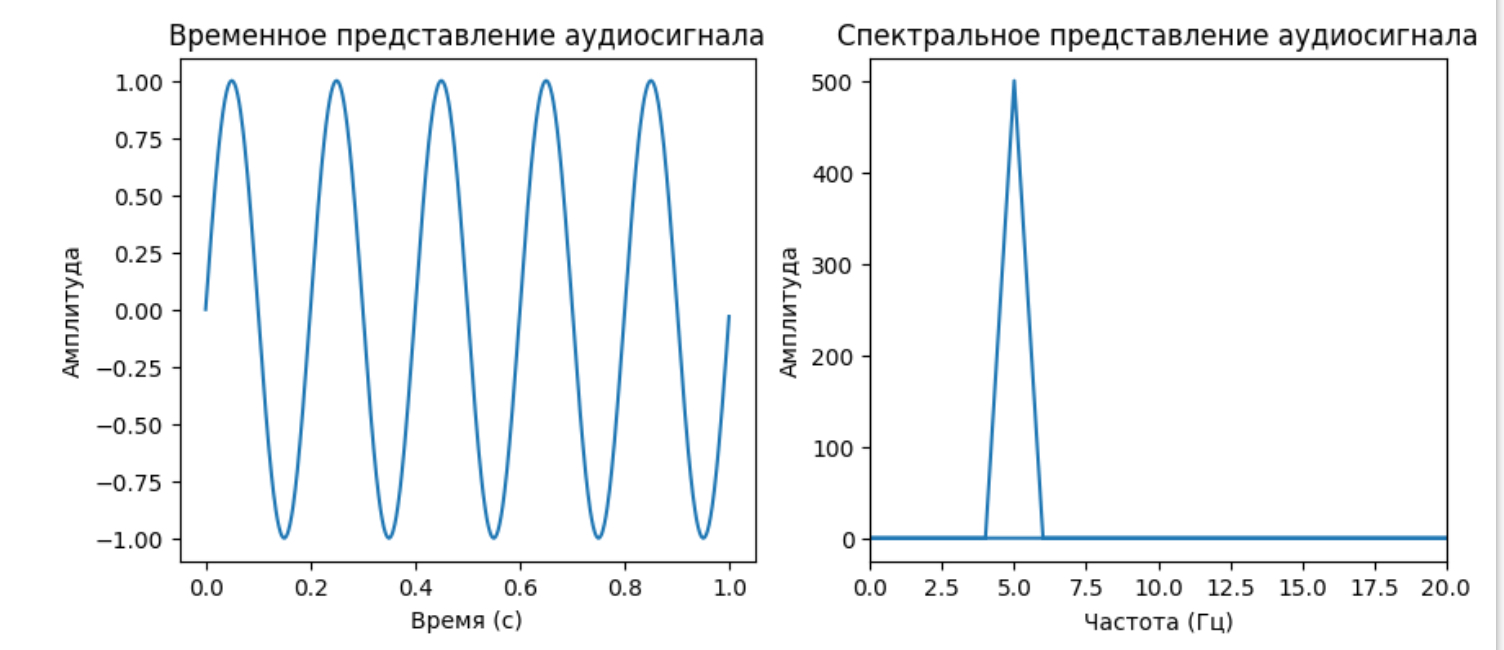 частотной области.

Преобразование Фурье в аудиотехнологиях:

В аудиотехнологиях часто используется быстрое преобразование Фурье (FFT), что позволяет эффективно вычислять спектр аудиосигнала в реальном времени. Оно является основой для многих алгоритмов аудиообработки, таких как эквалайзеры, компрессоры, реверберации и другие аудиоэффекты.

Преобразование Фурье играет важную роль в анализе и обработке аудиосигналов, обеспечивая возможность изучать и манипулировать спектральными характеристиками звуковых записей и создавать разнообразные аудиоэффекты.

Вейвлет-преобразование – это более продвинутый метод, который позволяет анализировать аудиосигналы на разных временных и частотных масштабах. Вейвлет-преобразование разлагает сигнал, используя вейвлет-функции, которые могут быть масштабированы и сдвинуты. Это позволяет выделять как быстрые, так и медленные изменения в сигнале, что особенно полезно при анализе звука с переменной частотой и интенсивностью.

Концепция Вейвлет-преобразования включает в себя несколько шагов, которые позволяют анализировать аудиосигналы на различных временных и частотных масштабах. Рассмотрим эти шаги более подробно:

1. Выбор вейвлета: Первым шагом является выбор подходящего вейвлета. Вейвлет – это специальная функция, которая используется для разложения сигнала. Разные вейвлеты могут быть более или менее подходящими для различных типов сигналов. Например, вейвлет Добеши (Daubechies) часто используется в аудиообработке.

2. Разложение сигнала: Сигнал разлагается на вейвлет-коэффициенты, используя выбранный вейвлет. Этот шаг включает в себя свертку сигнала с вейвлет-функцией и вычисление коэффициентов на разных масштабах и позициях во времени.

3. Выбор временных и частотных масштабов: Вейвлет-преобразование позволяет анализировать сигнал на различных временных и частотных масштабах. Это достигается за счет масштабирования и сдвига вейвлет-функции. Выбор конкретных масштабов зависит от задачи анализа.

4. Интерпретация коэффициентов: Полученные вейвлет-коэффициенты представляют собой информацию о том, какие временные и частотные компоненты присутствуют в сигнале. Это позволяет анализировать изменения в сигнале на разных временных и частотных масштабах.

5. Визуализация и интерпретация: Результаты Вейвлет-преобразования могут быть визуализированы, например, в виде спектрограммы вейвлет-коэффициентов. Это позволяет аналитику или исследователю видеть, какие частоты и временные изменения доминируют в сигнале.

Пример на Python для анализа аудиосигнала с использованием библиотеки PyWavelets:

```python

import pywt

import pywt.data

import numpy as np

import matplotlib.pyplot as plt

# Создаем пример аудиосигнала

signal = np.sin(2 * np.pi * np.linspace(0, 1, 1000))

# Выполняем Вейвлет-преобразование

coeffs = pywt.wavedec(signal, 'db1', level=5)

# Визуализируем результат

plt.figure(figsize=(12, 4))

plt.subplot(121)

plt.plot(signal)

plt.title('Исходный аудиосигнал')

plt.subplot(122)

plt.plot(coeffs[0]) # Детализирующие коэффициенты

plt.title('Вейвлет-коэффициенты')

plt.show()

```

В этом примере мы создаем простой синусоидальный аудиосигнал и выполняем Вейвлет-преобразование, используя вейвлет Добеши первого уровня. Полученные коэффициенты представляют информацию о различных временных и частотных компонентах сигнала.

Используя Вейвлет-преобразование, вы можете анализировать аудиосигналы на различных временных и частотных масштабах, что делает его мощным инструментом в аудиообработке и анализе звука.

Оба метода, преобразование Фурье и вейвлет-преобразование, имеют свои собственные преимущества и применения. Преобразование Фурье обеспечивает хороший спектральный анализ и используется в задачах, таких как эквалайзинг и анализ спектра. Вейвлет-преобразование более гибкое и позволяет анализировать сигналы с разной временной и частотной структурой, что полезно в аудиоинженерии и обнаружении аномалий.

В зависимости от конкретной задачи и требований анализа аудиосигнала, один из этих методов может быть более предпочтителен.

Глава 3: Основы нейросетей и глубокого обучения

3.1. Обзор архитектур нейросетей, включая сверточные и рекуррентные нейронные сети

Обзор архитектур нейронных сетей включает в себя разнообразные архитектуры, разработанные для решения различных задач машинного обучения. Среди них особенно выделяются сверточные и рекуррентные нейронные сети.

Сверточные нейронные сети (Convolutional Neural Networks, CNN)

Основное применение: Обработка изображений и видео, распознавание объектов, классификация и сегментация изображений.

Основные элементы: Сверточные слои, пулинг слои и полносвязные слои.

Принцип работы: Сверточные нейронные сети (CNN) – это специализированный вид нейронных сетей, разработанный для обработки изображений и других данных с сетчатой структурой, таких как видео или звук. Основной принцип работы CNN заключается в использовании сверточных слоев для извлечения признаков и пулинг слоев для уменьшения размерности данных.

Сверточные слои работают с помощью ядер свертки, которые скользят по входным данным и вычисляют взвешенную сумму значений в заданной области. Это позволяет выделить локальные шаблоны и структуры в данных, создавая карты признаков. После свертки применяется функция активации, обычно ReLU, чтобы внедрить нелинейность в модель.