Kitobni o'qish: «Рассуждения об основах физики»

Предисловие

Основой для написания этой книги послужила изданная в 2019 г. книга [1], а также восемь научных статей, опубликованных уже после выхода в свет указанной книги. Эти статьи являются логическим продолжением книги [1] и вместе образуют единое целое, которое мы и назвали «Рассуждения …». То, что речь идет об основаниях физики, вполне справедливо. Здесь мы будем говорить о самых основных понятиях физики: длине, времени, массе, скорости, об абсолютном и относительном (о заряде и спине мы будем говорить кратко, по ходу изложения). Мы также будем говорить о связи геометрии с физикой. Особое место отводится здесь проблеме измерения времени. Эта проблема, до сих пор спорная, теперь уже никак не может обойтись без критики теории относительности и гипотезы расширения Вселенной. И здесь мы покажем иллюзорность этих теорий.

Изложение принципиально ведется с позиций материалистического понимания законов природы и законов мышления. Эта книга будет полезна не только физикам и астрономам, но и математикам, а также и тем, кто намерен изучать законы природы вообще.

Замечание об обозначениях. В связи с особенностями цифровой печати, физическую (алгебраическую) величину скорость мы будем обозначать буквой V (прописной, латинский курсив), чтобы надежно отличать её от ν (ню – частота колебаний). Векторные величины будем обозначать как обычно – латинский шрифт, полужирный, строчной, прямой (r – радиус-вектор точки, v – вектор скорости точки и т. д.). В записях в строку будем применять косую черту, как символ деления: a/b означает a, деленное на b. В числовых записях символ * будет обозначать умножение.

Глава 1. Об измерении времени и основах теории относительности

1. 1. Постановка задачи

Среди многочисленных высказываний в физике у нас наибольшее беспокойство и недоумение вызывают два следующих постулата, лежащих в основах так называемой, специальной теории относительности. Они таковы. Во-первых, скорость материальной точки не может превышать скорости света [2, с. 358] (далее коротко – 1-й постулат); во-вторых, скорость света всегда одна и та же в любой системе координат [2, с. 365] (далее коротко – 2-й постулат). На практике обычно говорят только о втором постулате и называют его кратко – «постулат о постоянстве скорости света». Нумерация нам понадобилась, чтобы избежать путаницы в изложении.

Наша цель: выяснить, как могло случиться, что в теории относительности все скорости относительны, а скорость света, однако, абсолютна? А так ли это на самом деле? Как выяснилось по ходу размышлений, происхождение постулатов тесно связано с проблемами измерения времени. Поэтому мы начнем с того, что проанализируем заново работу часов, а для этого посмотрим на них более внимательно.

После этого мы обсудим вопросы, касающиеся одновременности событий, синхронизации часов, преобразований координат и, наконец, придем к выводу, что постулаты, о которых говорилось выше, не имеют места и не являются законами природы.

1. 2. Общая, традиционная точка зрения на принципы работы часов

Обозревая устройство различных часов, и помня о том, что любые часы можно заменить эквивалентными световыми часами, мы можем взглянуть на часы с одной общей точки зрения.

Общим для всех часов (часто в неявной форме) является наличие у них некоторой, так называемой, эталонной скорости (далее V_e).

Среди всех скоростей измеряемых физиками, существуют скорости, обладающие весьма высоким постоянством. Именно эти скорости и берутся для построения часов. Что делают часы? Они берут некоторый, всякий раз постоянный (то есть эталонный) отрезок длиной s_e и преобразуют его в эквивалентный временной интервал Δt по формуле: Δt = s_e/V_e. Постоянство V_e и s_e гарантирует также и постоянство Δt . Когда мы говорим: «часы берут отрезок s_e» под этим мы понимаем, что этот отрезок встроен в сами часы (то есть является их важнейшей частью). Это необходимо, чтобы часы могли работать, находясь в покое. Обычно преобразование отрезка s_e во время делается методом «туда и обратно» как световых часах. В них световой импульс, проходя путь равный 2s_e от генератора до зеркала и обратно, преобразуется во временной интервал: Δt = 2s_e/c. Здесь c – скорость света.

1. 3. Материальная точка и часы как преобразователи пространства во время

Далее мы будем рассматривать только прямолинейное движение материальных точек и часов вдоль оси OX. В пункте (1. 13.) мы дадим обобщение полученных результатов на трехмерное пространство.

Пусть материальная точка двигается по оси OX c некоторой скоростью V . Этот процесс можно рассматривать как преобразование пространства во время по закону x/V = t, то есть пройденному расстоянию x материальной точки ставится в соответствие некоторое время t = x/V. В частном случае, когда V = 0 можно считать, что это преобразование также имеет место, но его результат не определен.

Рассмотрим теперь часы, как и материальную точку, двигающиеся вдоль оси OX или покоящиеся. В чем сходство часов с материальной точкой? Их два. Первое – часы также материальны, как и материальная точка. Второе – часы также являются преобразователем пространства во время.

В чем отличие часов от материальной точки? Их два. Первое – часы преобразуют пространство во время, используя строго постоянную (эталонную) скорость V_e по закону: t = x/V_e, тогда как у материальной точки скорость, вообще говоря, может быть любой. Второе – часы, находясь в покое, сохраняют прежним результат преобразования: t = x/V_e, тогда как у покоящейся материальной точки результат преобразования становится неопределенным. Таким образом, чтобы получить представление о реальных (материальных) часах, мы должны скомбинировать и сходства и различия между часами и материальной точкой (непротиворечивым образом) в одном устройстве, называемом реальными часами.

Сделав это, мы получим структурную схему часов, изображенную на рис. 1. 1.

Рис. 1. 1

В преобразователе пространство – время (s -> t) на основе эталонной скорости V_e последовательно преобразуются эталоны длины s_e и часы показывают на выходе слагаемое N(s_e/V_e), где N – число периодов часов. Но если часы сдвигаются по оси OX на величину Δx, то и эту величину преобразователь также преобразует во время (по тому же закону) равное Δx/V_e. В результате часы будут на выходе показывать сумму:

Назовем слагаемое Δx/V_e слагаемым переноса часов. Слагаемое переноса равно нулю, если во время измерений часы неподвижны. Но если допустить, что часы не материальны (но все-таки работают), то в этом случае слагаемое переноса будет равно нулю и тогда, когда часы двигаются. Истинное время, измеренное часами, равно только N(s_e/V_e) и из показаний часов следует вычитать слагаемое переноса. Чтобы придать слагаемому переноса определенный знак (– или +) договоримся о направлении эталонной скорости V_e. Если часы сдвигаются независимо (от других скоростей), то будем направлять скорость V_e в положительном направлении оси OX. Если же часы двигаются вместе с материальной точкой, время движения которой они измеряют, то будем направлять скорость V_e также как и скорость точки V, то есть векторы v_e и v одинакового направления.

Рис. 1. 2

На рис. 1. 2 представлена наглядная механическая, одномерная модель реальных часов. Механизм часов двигается вдоль оси OX, не меняя своего направления в пространстве. Циферблат же часов, представляющий круг, может свободно вращаться вокруг своей оси и катиться по оси OX (для выполнения правила знаков он катится по оси OX снизу). Неподвижные часы (1) отсчитывают угол α пропорциональный истинному времени kα = N(s_e/V_e). Подвижные часы (2) отсчитывают угол α+β, причем β – угол поворота циферблата пропорционален слагаемому переноса, а k – коэффициент пропорциональности. Таким образом, подвижные часы отсчитают время:

В дальнейшем договоримся показания часов снабжать индексом χ (греческое хи), то есть писать – t_χ, тогда, как истинное время будем писать обычно – t и тогда:

Наиболее ясно механизм появления слагаемого переноса усматривается в световых часах. Если часы неподвижны, то путь проходимый светом за один период равен 2s_e. Но если часы двигаются вдоль оси OX (и световой импульс двигается вдоль этой же оси) то, как легко видеть, путь проходимый световым импульсом за один период будет равен не 2s_e, а равен 2s_e+Δx, где Δx – сдвиг часов за один период вдоль оси OX. Поэтому часы покажут время:

Здесь второе слагаемое есть слагаемое переноса часов.

1. 4. Система часов

На практике нам нужны не одни часы, а система часов, где все часы совершенно одинаковы. Чтобы достичь этого, нам необходима некоторая универсальная эталонная скорость V_e, обладающая тремя важными свойствами. Первое – она должна быть как можно более постоянна. Второе – она должна легко воспроизводиться. Третье – она должна быть как можно больше по величине. Если первое свойство весьма важно как в теоретическом и практическом отношениях, то второе и третье свойства важны лишь в практическом отношении. Именно такая универсальная скорость, как мы сейчас увидим, должна являться средством связи между часами, образующими систему часов.

Пусть в точках A и B расположены часы, которые должны работать совершенно одинаково. Расстояние AB = s. Каждые часы снабжаются генератором коротких импульсов, посылаемых к другим часам со скоростью V_e , а также генератором мгновенной отправки, пришедшего от других часов импульса в обратном направлении, имитируя отражение импульса. В случае световых импульсов генератор мгновенной отправки можно заменить отражающим зеркалом. Таким образом, каждые часы отправляют импульс к другим часам со скоростью V_e и получают его «отраженным» обратно с той же самой скоростью. Поэтому каждые часы должны показать одно и то же время движения импульса туда и обратно, равное: t = 2s/V_e. И если это не так, то вводятся поправочные коэффициенты, чтобы это было так (при необходимости к времени t добавляется «время задержки» импульса). Тем самым каждые часы приводятся к часам на основе одной универсальной скорости V_e (то есть заменяются по сути дела таковыми). Такая процедура создания системы часов не кажется простой, однако она легко объясняется. Не всякие часы можно расположить в одном месте, чтобы сверить их работу (например, на Марсе и на Земле) и, тем не менее, эти часы обязаны работать одинаково. Итак: универсальная эталонная скорость обязательно должна быть средством связи между часами, чтобы иметь гарантию идентичности часов системы. В настоящее время средством связи между часами является скорость света. Поэтому современную систему часов можно считать основанной на универсальной скорости (то есть единой для всех часов), скорости света:

V_e = c.

Далее для сохранения общности мы будем писать по-прежнему V_e, но в конкретных задачах мы всегда можем заменить V_e на c и это не должно приводить к недоразумениям.

Системы часов, основанные на разных универсальных скоростях, теоретически равносильны. Но на практике предпочтительна наибольшая из таких скоростей; при этом повышается точность измерения времени, а также сокращается время на создание системы часов.

1. 5. Синхронизация часов

Общепринятая практика синхронизации часов такова. Часы расставляются в исследуемые точки и в начало координат и регулируются следующим образом: из начала координат посылается световой импульс к регулируемым часам, находящимся в точке с координатой x. Наблюдатель, находящийся у этих часов, ставит время: t = x/c в момент получения светового импульса (c – скорость света).

Однако показания реальных часов включают в себя и слагаемое переноса часов, равное здесь также x/c. Поэтому на часах следует ставить время равное 2x/c. Синхронизированные таким образом, часы могут двигаться вдоль оси OX, и при этом слагаемое переноса будет меняться. Поэтому для правильного отсчета времени, кроме времени t_χ, всегда необходимо знать так же и координаты часов в момент измерения. И в этом заключается пространственно-временная связь.

Заметим еще, что предложенная здесь синхронизация часов не вполне корректна. Она основана на нашем твердом убеждении, что скорость света в одном направлении равняется средней скорости света на пути «туда и обратно». Но как это утверждение проверить экспериментально? Чтобы его проверить, необходимо иметь разведенные на расстояние s часы, синхронизированные ещё до начала опыта. И тогда вышеприведённый способ синхронизации уже не годится. В этом опыте нам придется двое часов расположить прежде в начале координат и запустить их одним начальным (нулевым) импульсом. После этого одни из часов сдвинуть по координате на расстояние s (не вмешиваясь в их работу). При этом в часах к истинному времени автоматически будет добавляться слагаемое переноса, которое при измерениях следует вычитать из показаний часов.

1. 6. Одновременные события

Рис. 1. 3

Одновременность событий поясняется на рис. 1. 3. Здесь в координатах XOt изображена зависимость от координаты слагаемого переноса x/V_e. Это прямая OC, наклонённая к оси OX под некоторым углом α, для которого tgα = 1/V_e. Назовем прямую OC прямой синхронизации. Прямая AB, параллельная прямой синхронизации замечательна тем, что события расположенные на ней одновременны, так как для точек этой прямой истинное время одинаково (например, t_A = t_B). Пусть теперь часы двигаются вместе с подвижной системой X^IO^It^I вдоль оси OX. При этом прямая синхронизации (теперь уже O^IC^I) будет сдвигаться параллельно прямой OC, а значит и параллельно прямой AB, а потому t^I_A = t^I_B. Из этого следует, что если в одной системе координат события A и B одновременны, то они будут одновременны и в другой системе координат.

Ввиду важности понятия одновременности остановимся на этом подробнее. Рассмотрим высказывание: пусть в момент времени t координаты точки равны x,y,z. В мире математики это высказывание есть не что иное, как определение неявной функции четырех переменных в виде F(x,y,z,t) = 0. Однако в мире физики это высказывание можно трактовать как угодно, если не сделать дополнительного соглашения (между физиками и математиками). Каково должно быть это соглашение? Оно должно быть таково, чтобы высказывания физика и математика относительно реального мира были тождественны. Это следующее соглашение: отметки на часах о времени события, а также отметки на координатных осях о положении точки должны делаться за время равное нулю (далее кратко, нуль – соглашение). Это соглашение необходимо и полезно, потому что теперь математический аппарат приобретает физический смысл. Это соглашение в неявной форме всегда присутствует в «правильных» формулах физики.

Однако сторонник теории относительности полагает, что отметки на осях координат можно делать за время равное нулю, а отметки на часах о времени события нельзя сделать за время равное нулю. Как он это узнал? Ведь материальная точка может находиться на очень большом удалении не только от часов, но и от осей координат. Эта непоследовательность (а точнее, отказ от нуль – соглашения) и привела к «релятивистскому» понятию одновременности, когда два одновременных события в одной системе координат становятся уже неодновременными в другой системе координат.

Конечно, на практике, как при измерении координат, так и при измерении времени, мы всегда используем конечные скорости распространения сигнала. Но наши формулы должны быть устроены так, чтобы они все равно приводили бы к выполнению нуль – соглашения. Если они к этому не приводят, значит – они неверны. Нам приходится об этом говорить, потому что об этом забывают.

Резюмируем сказанное. Наша точка зрения такова. Сторонники теории относительности нарушили нуль – соглашение и это привело к появлению многочисленных «парадоксов». Но это на самом деле не «парадоксы». Это настоящие противоречия, «парадоксами» мы их называем по традиции. Ни одно из этих противоречий не было и не могло быть удовлетворительно разрешено в рамках теории относительности. Многочисленные попытки разрешить эти противоречия – яркие примеры того, как нужно «правильно рассуждать неправильно». Это потому, что нельзя разрешить противоречие, выдвигаемое теорией, с помощью этой же самой теории.

1. 7. Скорость материальной точки

Пусть в начальный момент t_χ = t = 0 материальная точка двигается из начала координат вдоль оси OX со скоростью V. Вместе с ней с этой же скоростью двигаются и часы (V_e и V одного направления). Когда точка и часы будут находиться в точке с координатой x, часы покажут время t_χ. Это время состоит из двух слагаемых: 1-ое – истинное время движения точки t = x/V; 2-ое слагаемое – слагаемое переноса часов x/V_e. Таким образом:

Решая это уравнение относительно V, находим:

Эта формула отличается от обычной (классической) формулы наличием в знаменателе члена x/V_e и он появляется потому, что мы учитываем материальность часов. Для идеальных (нематериальных) часов этот член равен нулю. Заметим также, что соглашение о направлении скоростей V_e и V делает член x/V_e всегда положительным. Запишем (1. 3) с применением производных

Или

Таким образом, начиная с формул (1. 4) и (1. 5) нам следует отличать величины: – истинная (или исправленная) скорость точки, а 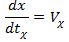– скорость этой же точки определяемая по показаниям часов традиционным методом, без учета материальности часов. Из (1. 5) видно также, что модуль скорости V всегда больше модуля скорости V_χ.

1. 8. Сложение скоростей

Пусть относительно системы координат O₁X₁ со скоростью V₁ движется другая система O₂X₂, а относительно системы O₂X₂ со скоростью V₂ движется материальная точка и вместе с ней с той же скоростью двигаются и часы. Какова скорость точки V относительно системы координат O₁X₁? В начальный момент времени t_χ = t = 0 положим координаты точки, часов и второй системы координат O₂X₂ равными нулю, относительно первой системы O₁X₁.

Время, отсчитанное часами по достижению точкой координаты x (в первой системе координат), равно 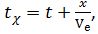а истинное время движения равно:

Путь, пройденный за это время системой O₂X₂ относительно системы O₁X₁ равен:

Путь, пройденный за это время точкой относительно системы O₂X₂, равен:

Путь, пройденный за это время точкой относительно системы O₁X₁ равен:

Этот путь равен сумме путей x₁ и x₂ , то есть:

x = x₁ + x₂.

Из последних четырех равенств получаем:

Итак, для истинных времени и скоростей правило сложения скоростей классической механики остается в силе и никаких ограничений на величины скоростей при этом не накладывается.

С применением формулы (1. 6) нетрудно вывести аналогичную формулу и для векторов скоростей:

1. 9. Первый постулат

Как уже говорилось выше, для современной системы часов V_e = c. Заменим в (1. 5) V_e на c и получим:

отсюда, выразив V_χ через V и c получим:

Пусть в выражении (1. 8) скорость V неограниченно возрастает. Тогда мы получим следующий предел:

Выражение (1. 9) есть не что иное, как математическая запись 1-го постулата, именно: если скорость точки измерять по показаниям часов t_χ, то измеренная таким способом скорость V_χ, никогда не превысит скорости света. При этом истинная скорость точки V может превышать скорость света на сколько угодно. Итак, 1-й постулат появился только потому, что измеряя время реальными часами, мы полагаем, что они – идеальны. При учете материальности часов и введении формул перехода от показаний часов к истинному времени, 1-й постулат теряет силу и должен быть отменен.

1. 10. Преобразования координат

При справедливости формул сложения скоростей (1. 6) и (1. 7), нетрудно сделать вывод, что уравнения классической механики, в том числе законы сохранения импульса и энергии, остаются в классической форме, и во всех формулах должно фигурировать истинное время t. То же самое относится и к производным по времени, например:

Преобразования координат есть преобразования Галилея, с добавлением формулы перехода от показаний часов к истинному времени: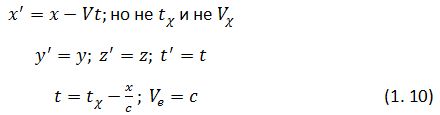

1. 11. Измерение массы ядер

В качестве примера того, как путаница между скоростями V_χ и V приводит к «странным» результатам, рассмотрим измерение масс ядер в масс-спектрометрах с применением магнитного поля. Измерение основано на приравнивании центростремительной силы силе Лоренца для частицы, движущейся в магнитном поле. Это уравнение таково:

Здесь: m – масса частицы, q – её заряд, r – радиус траектории частицы, B – индукция магнитного поля, V – скорость частицы.

Во времена Лоренца различие между V_χ и V не делалось, поэтому фактически уравнение (1.11) выглядит так:

Но теперь, когда мы знаем, что в центростремительную силу следует подставлять не V_χ, а V равное

то исправленное уравнение для измерения массы будет уже другим:

Здесь m^I – масса, измеренная с использованием уравнения (1. 13). Поделив (1. 12) на (1. 13) найдем отношение масс:

Поскольку с уменьшением массы частицы ее скорость V_χ в приборе возрастает, то из (1. 14) следует, что завышение массы, измеренное при помощи уравнения (1. 12) возрастает по отношению к массе, измеренной при помощи уравнения (1. 13) с уменьшением массы исследуемой частицы. Что нам следует ожидать, если при измерении масс ядер мы будем использовать уравнение (1. 13), а не (1. 12)? Нам следует ожидать, что, так называемый, «дефицит масс» станет равен нулю, а закон сохранения массы будет иметь силу и для микрочастиц.